Existing solutions to the problem of autonomously disinfecting rooms using UV light rely on manually selecting a single vantage point in the room and allowing the UV light to emit for a fixed amount of time. Usually, they pick a point in the center of the room’s obstacles. But there are a couple of issues with this paradigm. By the inverse square law of light, the radiation dose received by a surface decreases with the square of its distance to the source of light, so single point methods would struggle to disinfect far-off surfaces in a timely manner. Another issue to consider is occlusions, or objects that block the passage of light. In any realistic room-model, light will simply be unable to reach all desired surfaces from a single point, leaving parts of the room still infected.

Our method of disinfection avoids these issues and manages to minimize the dwell-time needed to actually disinfect all surfaces in the room, and gets somewhat close to optimizing a path through these points. In order to argue for why our method is superior, though, examples and actual data always help. So, I spent a couple days this week simulating single-point solutions and calculating how good of a job they did, along with how much time they took to disinfect the room. In this simulation, I assumed that all edges are non-opaque, so they let light through, even through the insides of obstacles. Then, I found the two points; the centroid of the obstacle nodes, and the grid-point (from when we griderize our space) which minimizes dwell-time at it.

NOTE: Even though this is an invalid assumption (i.e. it would never happen in real life), doing this gives our method an even better argument. The actual single-point dwell-time is bounded below by the dwell-time assuming non-opaqueness. If our method performs better than this bound, then we’re doing better even giving the best possible hypothetical scenario to the current paradigm.

Here’s an sample single-point solution assuming that light goes through edges and obstacles:

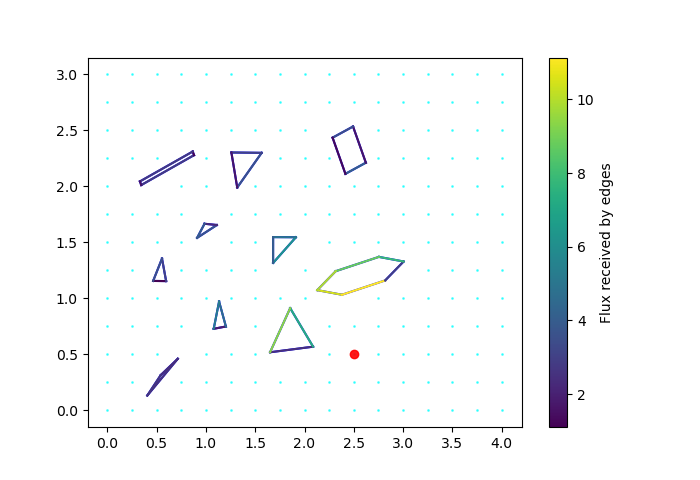
Unsurprisingly, our solution did in fact, do far better than the current paradigm in both scenarios, even taking into account the robot’s traversal time. These details and results were great for our argument, and we compiled them to present to the overall COVID-19 meeting (last meeting was three weeks ago). The external people seemed pretty happy with the results. There were a couple of other things discussed in the meeting. Someone mentioned it might be good to have a different linear programming setup where we maximize the amount of flux received by edges if we have a bound on the total dwell-time. This might be useful in cases where total disinfection takes very long, or in cases where we aren’t allowed a lot of time to disinfect.

In our weekly meeting, one of Prof. Hauser’s postdocs, Zherong Pan, mentioned that he had a mixed integer linear programming formulation for minimizing total disinfection time. This includes the dwell-time and the time taken to move around the tour which reaches each of these points. This was pretty exciting! This is the actual minimization we want – no approximations at all. Now, the problem is that mixed integer linear programs can’t necessarily be solved in polynomial time.

NOTE: A mixed integer linear program (MILP) is very similar to a linear program. We optimize for a linear expression of our decision variables, while enforcing constraints that can be described by linear expressions of these variables. However, there are additional constraints for some variables. In a linear program, all variables can take continuous values, i.e. they are assumed to be real values (although they can be bounded by constraints). In a MILP, some of these variables are further constrained to be only integers. For example, a MILP might have variable x which we bound by linear constraints to be between 0 and 1 (inclusive). If the MILP further constraints x to be an integer, then we know it can only take binary values (0 or 1). This small change actually makes MILPs much harder to solve! Integer linear programming is NP-complete, making it typically a much more costly program (time-wise) to solve.

However, this is great news in terms of our tests! With the MILP, we can find the actual optimal disinfection time. This gives us a base value to test our algorithm (which just uses an LP) against. If it does well, this is perhaps the best argument towards using our quick and hopefully close-to-optimal algorithm.

These developments and ideas gave me lots of directions to follow. However, before starting these problems, I worked on testing a heuristic for potential vantage-point selection. One of the main bottle-necks for our algorithms’ run-time has been vantage-point visibility graph calculations. However, from lots of our solutions, we’ve noted that the dwell-points selected are never far off from the obstacles; usually, the points get selected very close by. Finding visibility graphs for all these points that aren’t ever chosen is therefore wasted computation time. There’s also the future consideration that in three dimensions, gridding the space is infeasible both in terms of memory and time. Even in two dimensions, the program struggles to complete at very high resolution and visibility computations are more complicated in three dimensions.

The first heuristic I tested was selecting points on the perpendicular bisectors of each obstacle edge, at some required minimum distance away. I completed this heuristic code, but testing has turned out to be a longer deal than I expected. For a fair comparison, I want to find dwell-times for the optimal solution (using the grid) at as high a resolution I can. But the run-times are ridiculously long, so I plan to let them run over the weekend and see what happens.